Laminar inference with OPM data

This tutorial demonstrates how to perform laminar inference using model comparison based on free energy using simulated OPM data, as shown in [Helbling, 2025, Inferring laminar origins of MEG signals with optically pumped magnetometers (OPMs): A simulation study](https://direct.mit.edu/imag/article/doi/10.1162/imag_a_00410/125546). As in tutorial 02, a 20Hz oscillation is simulated at a particular cortical location in various layers. Source reconstruction is performed using the Empirical Bayesian Beamformer on the simulated sensor data using forward models based on different layer meshes. These models are then compared using free energy.

Setting up the OPM simulations

Simulations are based on a synthetic OPM dataset, which is used to define the sampling rate, number of trials, duration of each trial, and the channel layout.

import os
import shutil
import tempfile
from IPython.display import Image
import base64

import numpy as np
import matplotlib.pyplot as plt
from lameg.invert import coregister, invert_ebb
from lameg.laminar import model_comparison
from lameg.simulate import run_current_density_simulation, setup_opm_simulation
from lameg.surf import LayerSurfaceSet
from lameg.util import get_fiducial_coords
from lameg.viz import color_map, show_surface
import spm_standalone

# Subject information for data to use
subj_id = 'sub-104'
ses_id = 'ses-01'

# Fiducial coil coordinates
fid_coords = get_fiducial_coords(subj_id, '../test_data/participants.tsv')

# Where to put simulated data
tmp_dir = tempfile.mkdtemp()

spm = spm_standalone.initialize()

The simulations will be based on a forward model using the multilayer mesh, and the model comparison will use each layer mesh

surf_set_bilam = LayerSurfaceSet(subj_id, 2)
surf_set = LayerSurfaceSet(subj_id, 11)

Instead of using an existing MEG dataset as a template, we will now generate a new synthetic OPM dataset directly using lameg.simulate.setup_opm_simulation(). This function configures and runs SPM’s OPM simulation utility (spm_opm_sim), which creates a valid SPM MEEG object containing empty data arrays with the desired sampling rate, number of trials, and sensor configuration.

We will generate 200 trials of 1 second each (600 samples per trial), using triaxial sensors distributed over the superior half of the scalp. The simulated sensor array will be placed 3.5 mm above the scalp surface, with 35 mm spacing between adjacent sensors.

The resulting .mat and .dat files will serve as the base dataset for subsequent simulations, laminar model inversion and, free energy comparison.

s_rate = 600

base_fname = setup_opm_simulation(
    os.path.join(tmp_dir, 'test_opm'),
    surf_set,
    s_rate=s_rate,
    wholehead=False,
    sensor_spacing=35,
    sensor_offset=3.5,
    n_samples=s_rate,
    n_trials=200,
    axes=3,
    spm_instance=spm
)

The rest of the tutorial is the same as tutorial 02 - we just now work with this base synthetic OPM dataset.

Invert the subject’s data using the multilayer mesh. This step only has to be done once - this is just to compute the forward model that will be used in the simulations

# Patch size to use for inversion (in this case it matches the simulated patch size)
patch_size = 5
# Number of temporal modes to use for EBB inversion
n_temp_modes = 4

# Coregister data to multilayer mesh
coregister(
    fid_coords,
    base_fname,
    surf_set,
    spm_instance=spm
)

# Run inversion
[_,_] = invert_ebb(
    base_fname,
    surf_set,
    patch_size=patch_size,
    n_temp_modes=n_temp_modes,
    n_spatial_modes=60,
    spm_instance=spm
)

Simulating a signal on the pial surface

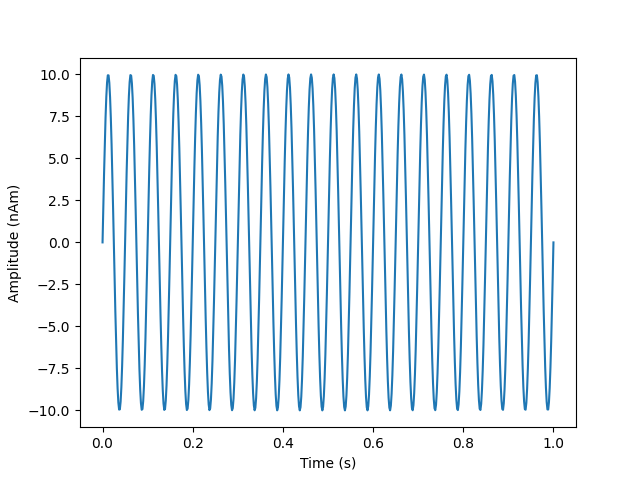
We’re going to simulate 1s of a 20Hz sine wave with a dipole moment of 10nAm

# Frequency of simulated sinusoid (Hz)
freq = 20
# Strength of simulated activity (nAm)
dipole_moment = 10

# Generate 1s of a sine wave at a sampling rate of 600Hz (to match the data file)
time = np.linspace(0,1,s_rate)
sim_signal = np.sin(time*freq*2*np.pi).reshape(1,-1)

plt.plot(time,dipole_moment*sim_signal[0,:])
plt.xlabel('Time (s)')
plt.ylabel('Amplitude (nAm)')

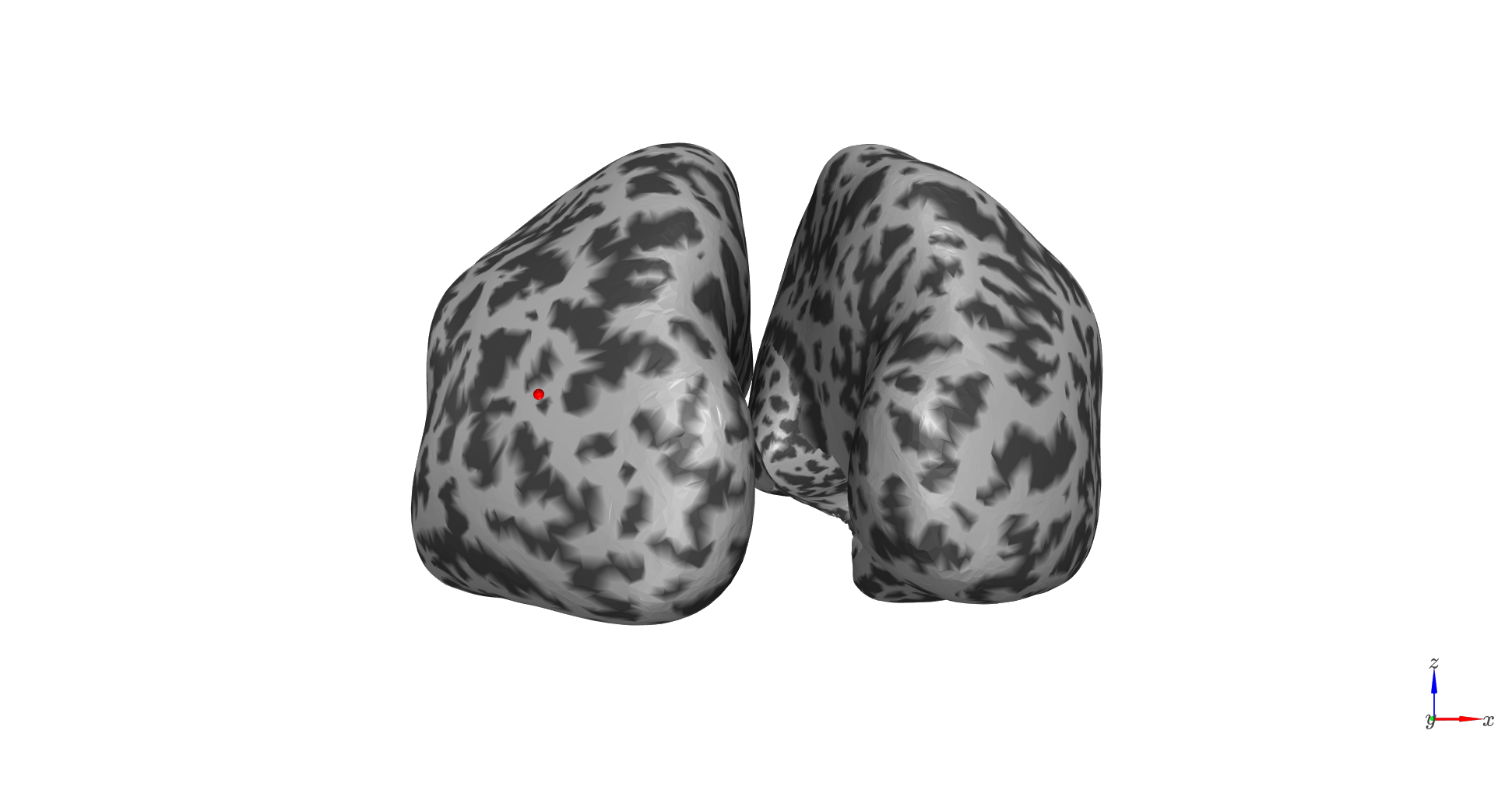
We need to pick a location (mesh vertex) to simulate at

sim_vertex=10561

cam_view = [40, -240, 25,
            60, 37, 17,
            0, 0, 1]
plot = show_surface(
    surf_set,
    marker_vertices=sim_vertex,
    marker_size=5,
    camera_view=cam_view
)

We’ll simulate a 5mm patch of activity with -5 dB SNR at the sensor level. The desired level of SNR is achieved by adding white noise to the projected sensor signals

# Simulate at a vertex on the pial surface
pial_vertex = surf_set.get_multilayer_vertex('pial', sim_vertex)
prefix = f'sim_{sim_vertex}_pial_'

# Size of simulated patch of activity (mm)
sim_patch_size = 5
# SNR of simulated data (dB)
SNR = -5

# Generate simulated data
pial_sim_fname = run_current_density_simulation(
    base_fname,
    prefix,
    pial_vertex,
    sim_signal,
    dipole_moment,
    sim_patch_size,
    SNR,
    spm_instance=spm
)

Model comparison (pial - white matter)

Now we can run model comparison between source models based on the pial and white matter surfaces using free energy. Specifically, we’ll look at the difference in free energy between the two models (pial - white matter). This should be positive (more model evidence for the pial surface model) because we simulated activity on the pial surface

# Run model comparison between the first layer (pial) and the last layer (white matter)
[F,_] = model_comparison(
    fid_coords,
    pial_sim_fname,
    surf_set_bilam,
    spm_instance=spm,
    invert_kwargs={
        'patch_size': patch_size,
        'n_temp_modes': n_temp_modes,
        'n_spatial_modes': 60
    }
)

The difference in free energy is an approximation of the Bayes factor between the two models This value should be positive (more model evidence for the pial layer model)

F[0]-F[1]

White matter surface simulation with pial - white matter model comparison

Let’s simulate the same pattern of activity, in the same location, but on the white matter surface. This time, model comparison should yield greater model evidence for the white matter surface, and therefore the difference in free energy (pial - white matter) should be negative.

# Simulate at the corresponding vertex on the white matter surface
white_vertex = surf_set.get_multilayer_vertex('white', sim_vertex)
prefix = f'sim_{sim_vertex}_white_'

# Generate simulated data
white_sim_fname = run_current_density_simulation(
    base_fname,
    prefix,
    white_vertex,
    sim_signal,
    dipole_moment,
    sim_patch_size,
    SNR,
    spm_instance=spm
)
# Run model comparison between the first layer (pial) and the last layer (white matter)
[F,_] = model_comparison(
    fid_coords,
    white_sim_fname,
    surf_set_bilam,
    spm_instance=spm,
    invert_kwargs={
        'patch_size': patch_size,
        'n_temp_modes': n_temp_modes,
        'n_spatial_modes': 60
    }
)

The difference in free energy is an approximation of the Bayes factor between the two models This value should be negative (more model evidence for the white matter layer model)

F[0]-F[1]

Simulation in each layer with model comparison across layers

That was model comparison with two candidate models: one based on the white matter surface, and one on the pial. Let’s now simulate on each layer, and for each simulation, run model comparison across all layers. We’ll turn off SPM visualization here.

# Now simulate at the corresponding vertex on each layer, and for each simulation, run model comparison across
# all layers
all_layerF = []

for l in range(surf_set.n_layers):
    print(f'Simulating in layer {l}')
    l_vertex = surf_set.get_multilayer_vertex(l, sim_vertex)
    prefix = f'sim_{sim_vertex}_{l}_'

    l_sim_fname = run_current_density_simulation(
        base_fname,
        prefix,
        l_vertex,
        sim_signal,
        dipole_moment,
        sim_patch_size,
        SNR,
        spm_instance=spm
    )

    [layerF,_] = model_comparison(
        fid_coords,
        l_sim_fname,
        surf_set,
        viz=False,
        spm_instance=spm,
        invert_kwargs={
            'patch_size': patch_size,
            'n_temp_modes': n_temp_modes,
            'n_spatial_modes': 60
        }
    )
    all_layerF.append(layerF)
all_layerF = np.array(all_layerF)

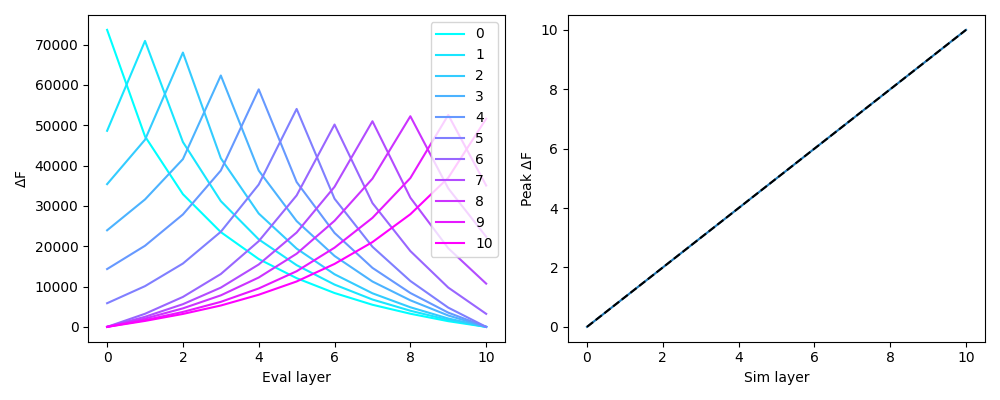
For each simulation, we can plot the free energy for all models relative to the worst model. The layer model with the highest free energy should correspond to the layer that the activity was simulated in.

col_r = plt.cm.cool(np.linspace(0,1, num=surf_set.n_layers))
plt.figure(figsize=(10,4))

# For each simulation, plot the free energy of each layer model relative to that of the worst
# model for that simulation
plt.subplot(1,2,1)
for l in range(surf_set.n_layers):
    layerF = all_layerF[l,:]
    plt.plot(layerF-np.min(layerF), label=f'{l}', color=col_r[l,:])
plt.legend()
plt.xlabel('Eval layer')
plt.ylabel(r'$\Delta$F')

# For each simulation, find which layer model had the greatest free energy
plt.subplot(1,2,2)
peaks = []
for l in range(surf_set.n_layers):
    layerF = all_layerF[l,:]
    pk = np.argmax(layerF)
    peaks.append(pk)
plt.plot(peaks)
plt.xlim([-0.5,10.5])
plt.ylim([-0.5,10.5])
plt.plot([0,10],[0,10],'k--')
plt.xlabel('Sim layer')
plt.ylabel(r'Peak $\Delta$F')
plt.tight_layout()

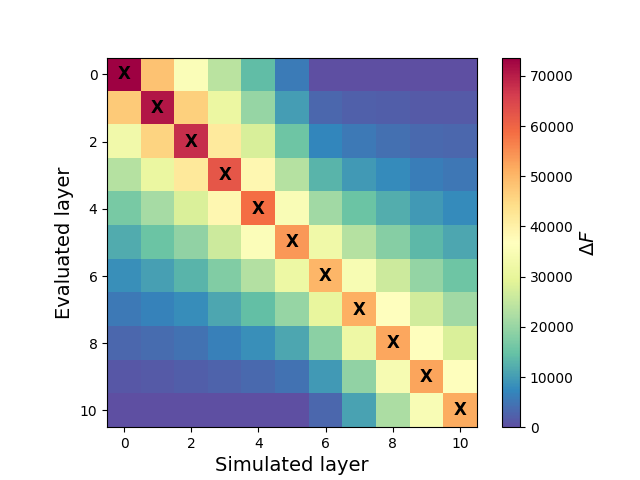
# Normalization step
norm_layerF = np.zeros(all_layerF.shape)
for l in range(surf_set.n_layers):
    norm_layerF[l,:] = all_layerF[l,:] - np.min(all_layerF[l,:])

# Transpose for visualization
im=plt.imshow(norm_layerF.T,cmap='Spectral_r')

# Find the indices of the max value in each column
max_indices = np.argmax(norm_layerF, axis=1)

# Plot an 'X' at the center of the square for each column's maximum
for idx, max_idx in enumerate(max_indices):
    plt.text(idx, max_idx, 'X', fontsize=12, ha='center', va='center', color='black', weight='bold')

plt.xlabel('Simulated layer', fontsize=14)
plt.ylabel('Evaluated layer', fontsize=14)
cb=plt.colorbar(im)
cb.set_label(r'$\Delta F$', fontsize=14)

spm.terminate()

# Delete simulation files
shutil.rmtree(tmp_dir)