Note

Go to the end to download the full example code

Surface processing#

This tutorial walks through the key steps involved in preparing laminar surfaces for MEG source reconstruction using laMEG. Starting from FreeSurfer outputs, we will generate multiple cortical layers, remove non-cortical vertices, merge hemispheres, downsample the meshes while preserving vertex correspondence, compute dipole orientations, and finally combine all layers into a single laminar surface model.

These operations are essential to obtain geometrically accurate, computationally efficient, and laminar-consistent source spaces.

Create layer surfaces#

The first step is to generate a set of intermediate surfaces between the pial and white matter boundaries.

This step: - Uses FreeSurfer’s mris_inflate utility to iteratively create surfaces that are approximately equidistant between the white and pial boundaries. - Maintains vertex correspondence across all layers: each vertex in the white surface is connected to its pial counterpart by a straight vector, and intermediate layer vertices lie along this line. - Converts each generated surface to GIFTI format and adjusts its coordinates using the FreeSurfer RAS offset (CRAS), ensuring that surfaces are in native anatomical space.

The resulting surfaces represent an anatomically consistent sampling of the cortical ribbon.

import numpy as np
import k3d
import matplotlib.pyplot as plt
from lameg.surf import LayerSurfaceSet
from lameg.viz import show_surface, rgbtoint

surf_set = LayerSurfaceSet('sub-104', 11)
layer_names = surf_set.get_layer_names()

cam_view=[-143, 14, 31.5,
          -32, 22.5, 38.5,
          0, 0, 1]
col_r = plt.cm.cool(np.linspace(0,1, num=surf_set.n_layers))

for l_idx,layer_name in enumerate(layer_names):
    plot = show_surface(
        surf_set,
        layer_name=layer_name,
        stage='converted',
        hemi='lh',
        plot_curvature=False,
        camera_view=cam_view,
        color=col_r[l_idx,:3]*255,
        height=256
    )

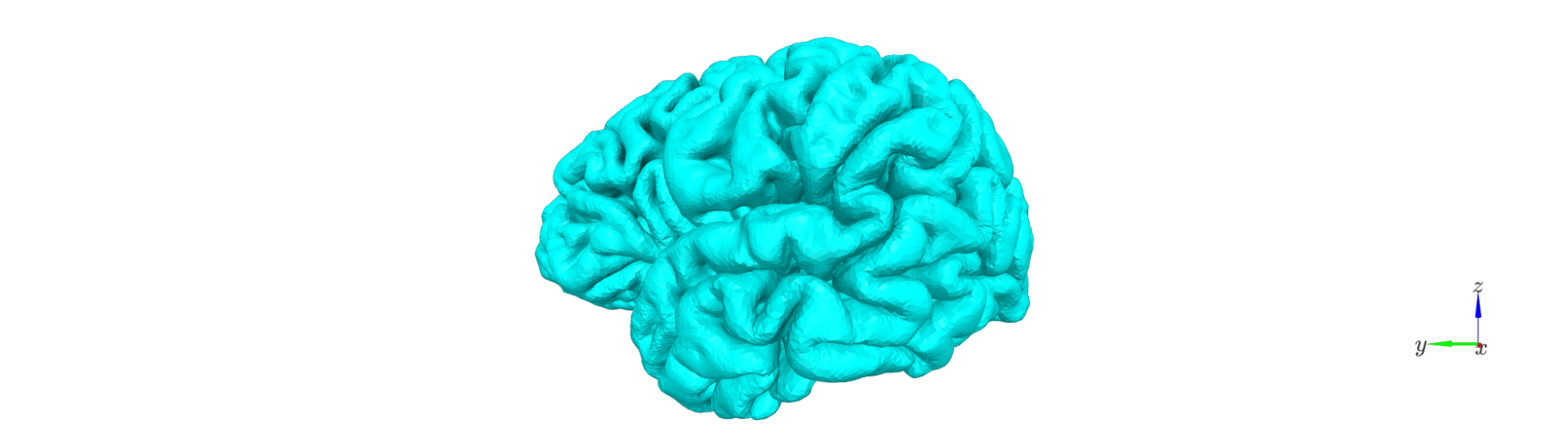
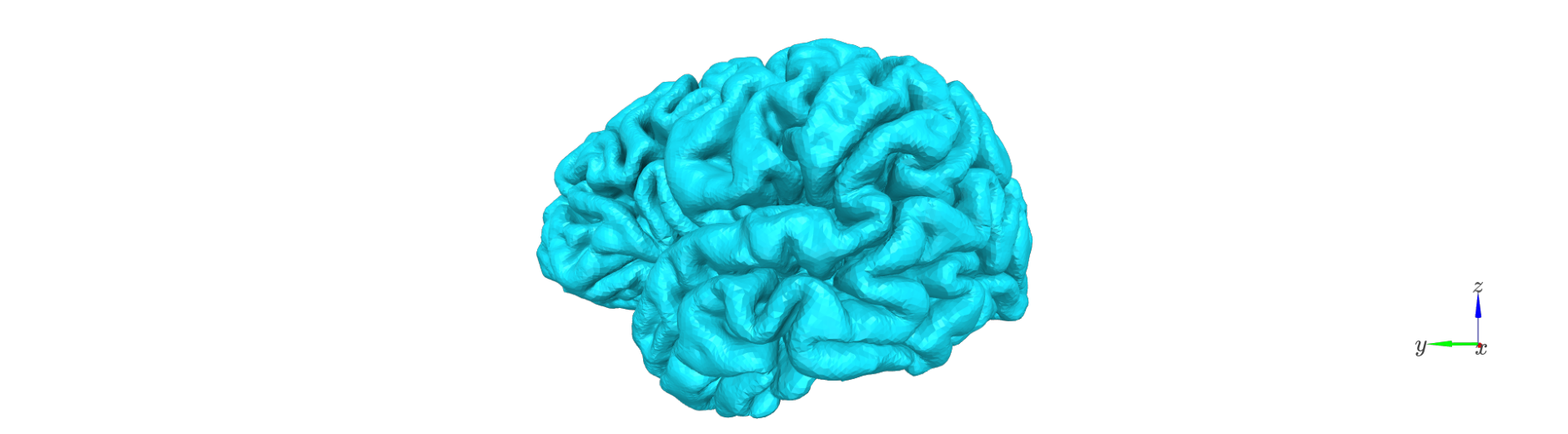
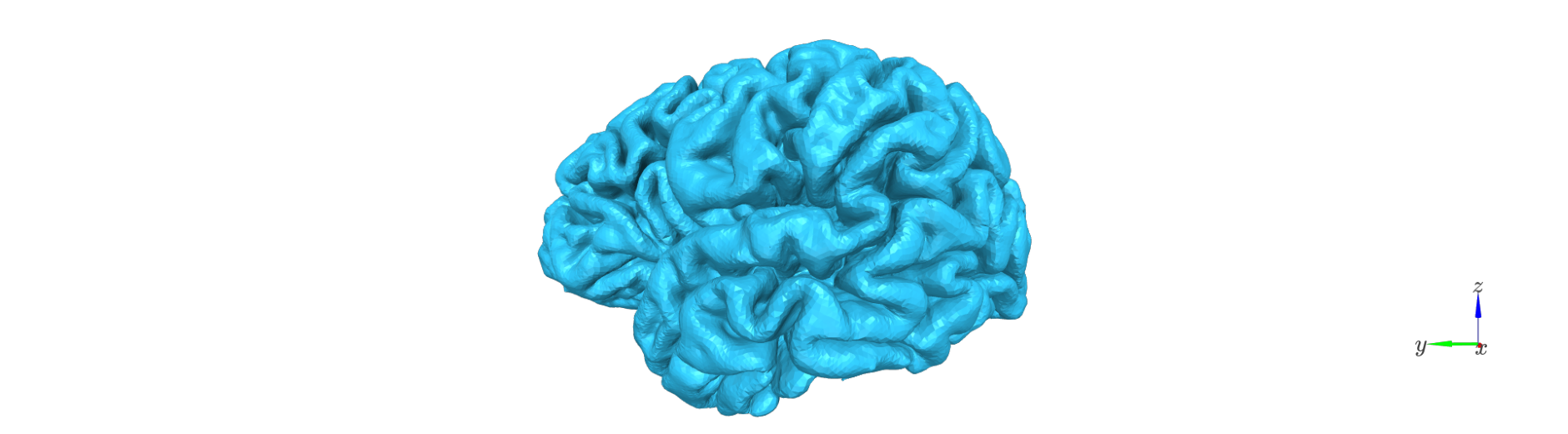
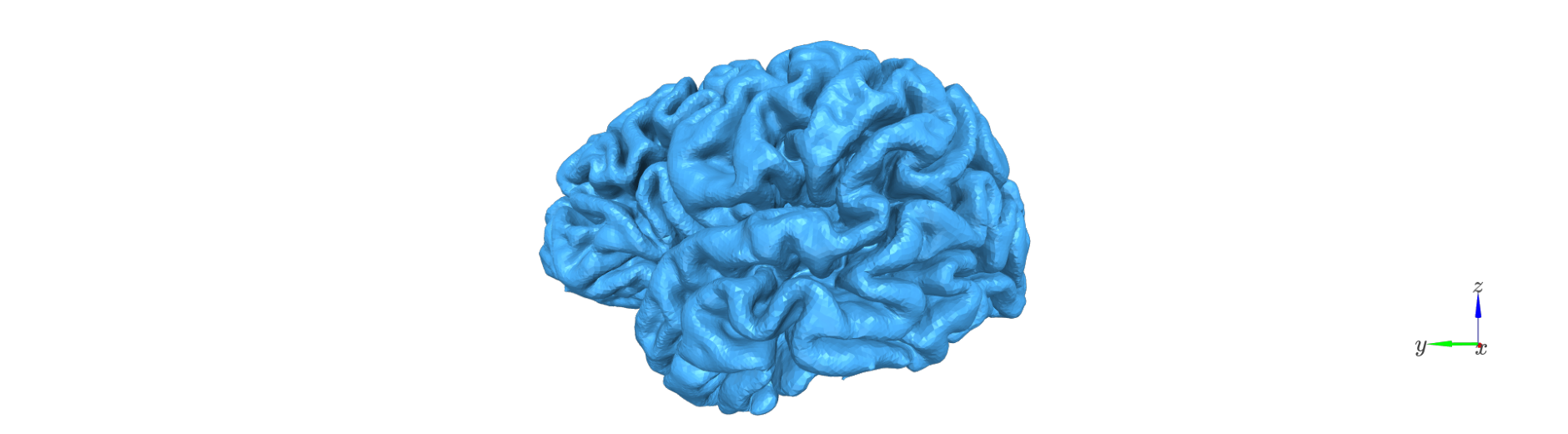
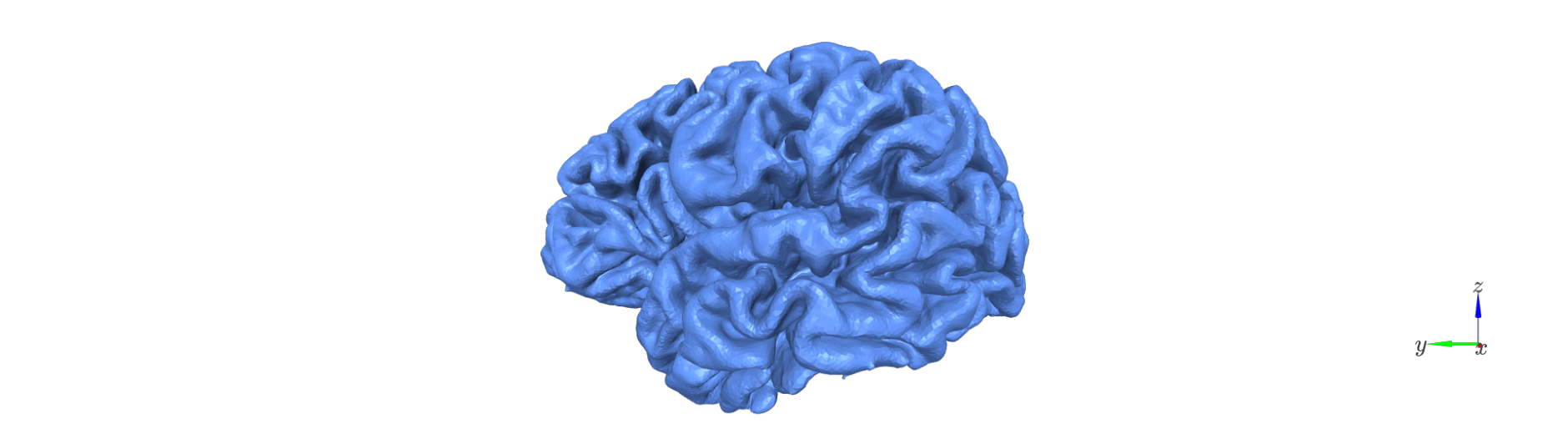
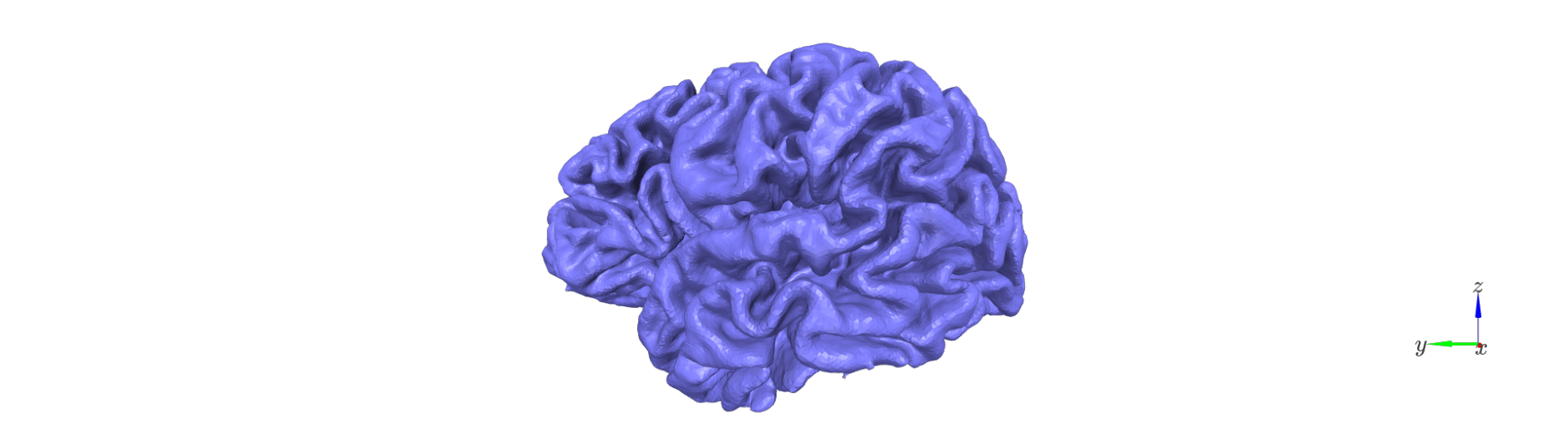
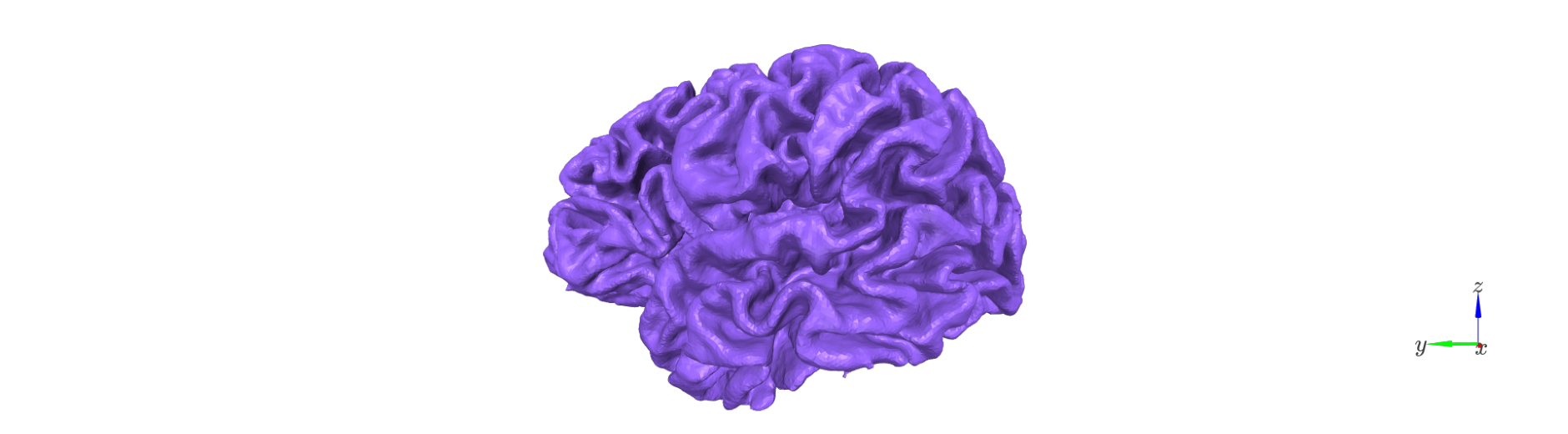
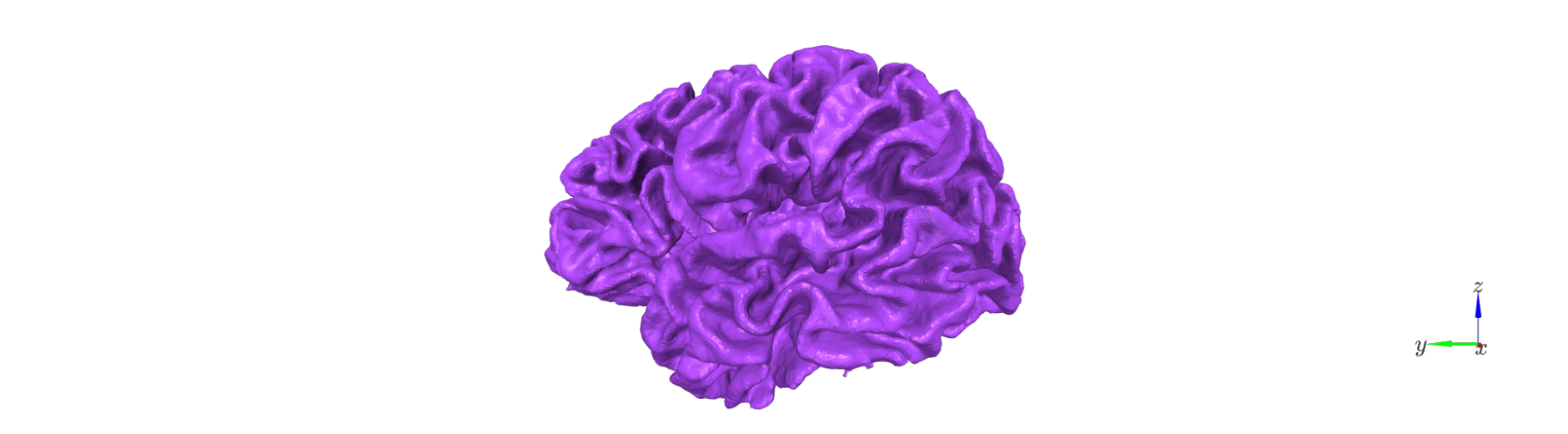
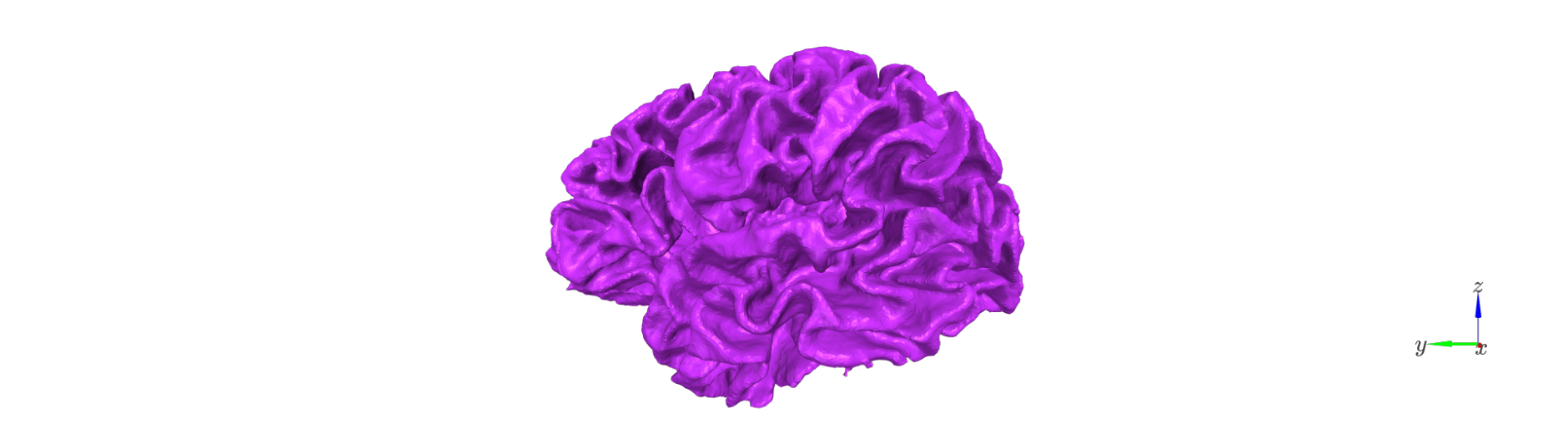
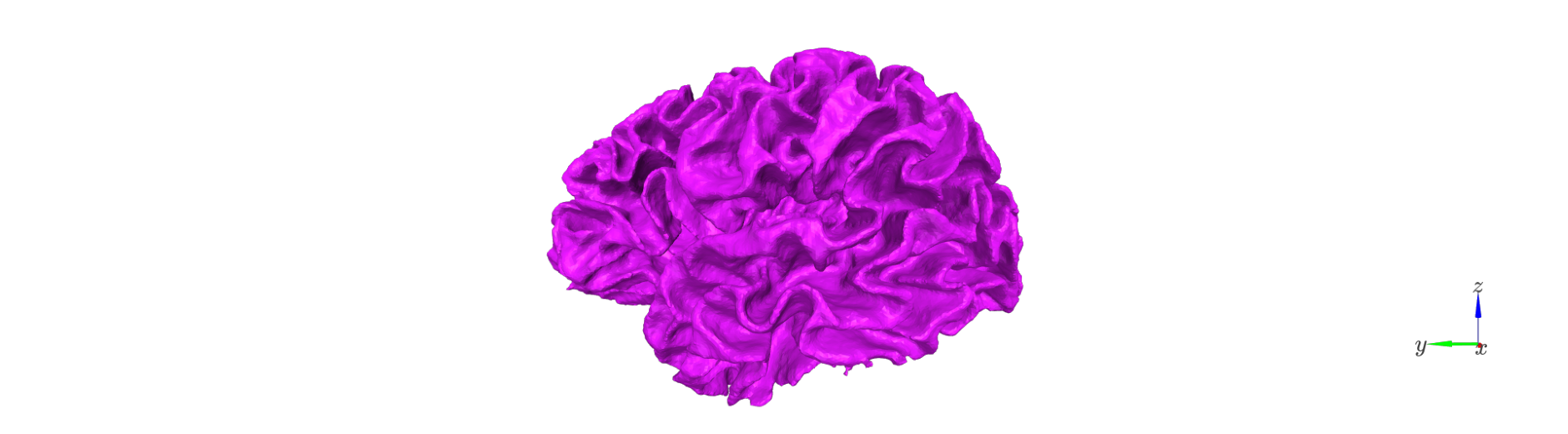
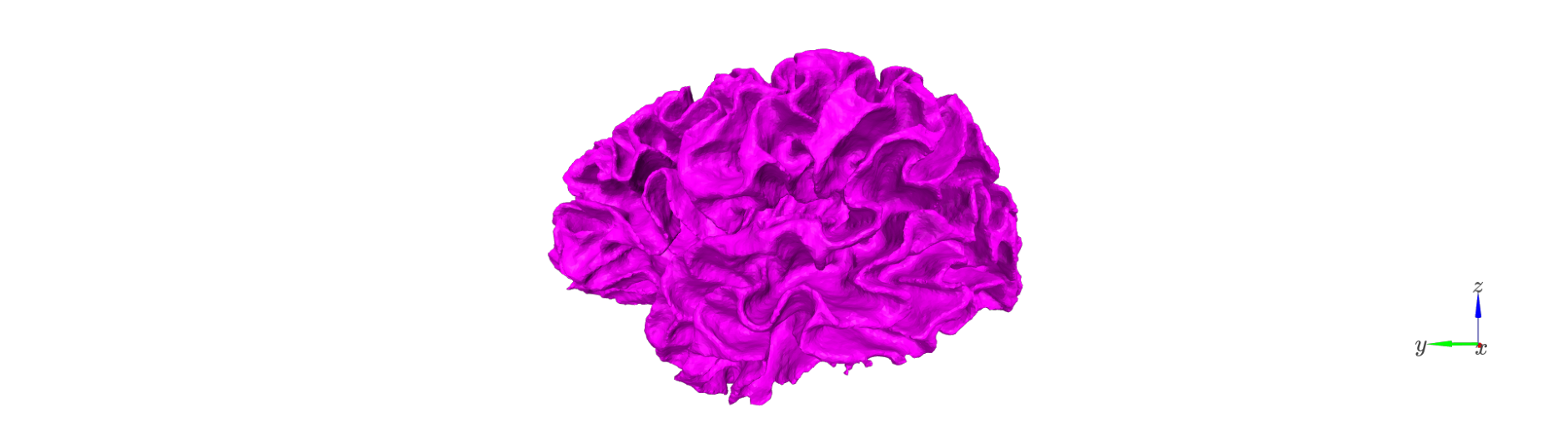
Remove deep vertices#

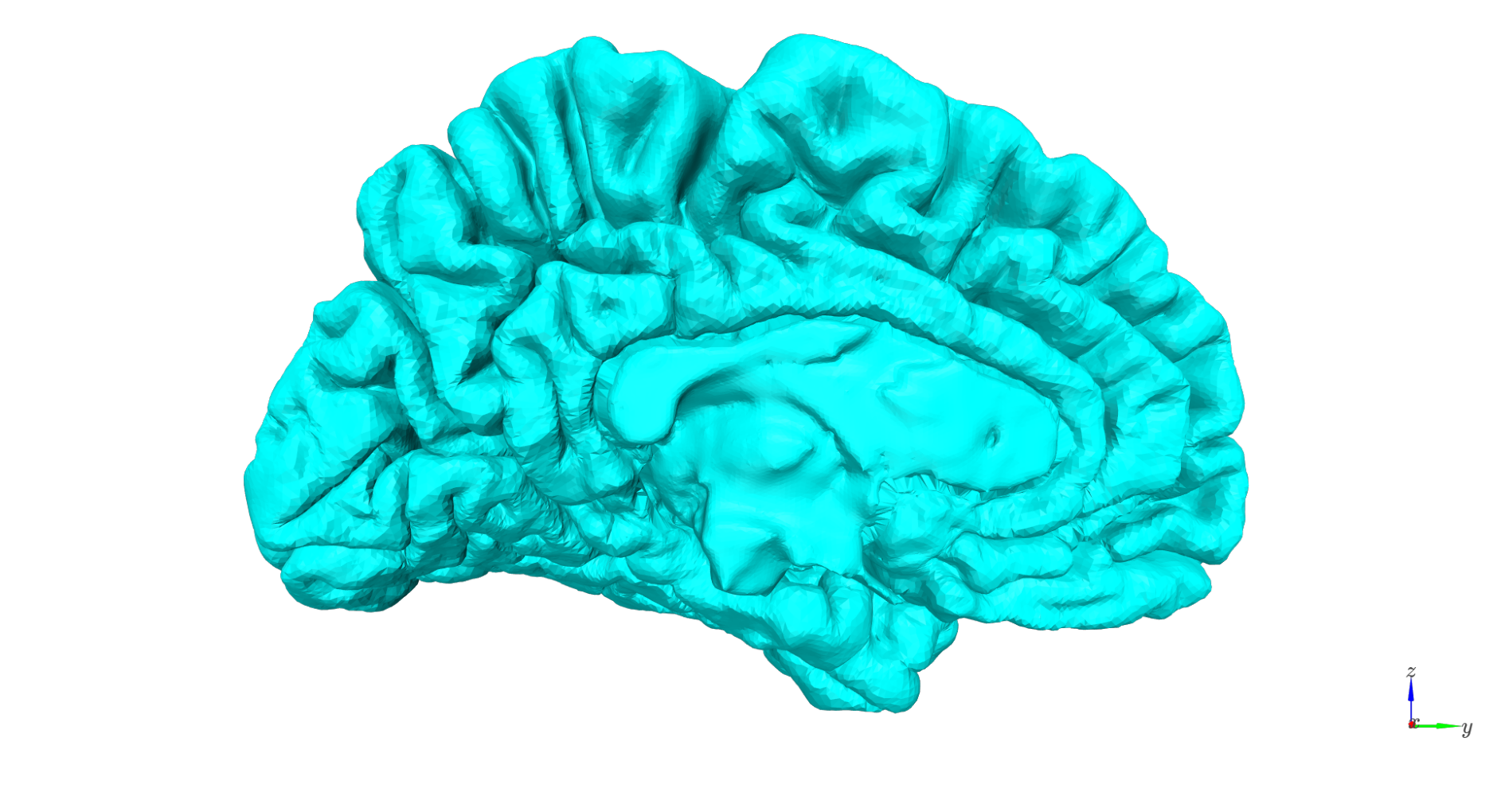
FreeSurfer surfaces include vertices that extend into deep structures (e.g., the corpus callosum), which are not part of the cortical source space.

This step removes those deep vertices and any associated faces by: - Identifying vertices not assigned to a cortical label in the Desikan-Killiany atlas. - Removing vertices labeled as “unknown”. - Applying this filtering independently to each hemisphere and each layer.

The resulting surfaces strictly represent cortical gray matter.

Before: deep vertices are visible within subcortical regions.

cam_view=[110, 18, 36,
          -32, 22, 42,
          0, 0, 1]
plot = show_surface(
    surf_set,
    layer_name='pial',
    stage='converted',
    hemi='lh',
    plot_curvature=False,
    camera_view=cam_view,
    color=col_r[0,:3]*255
)

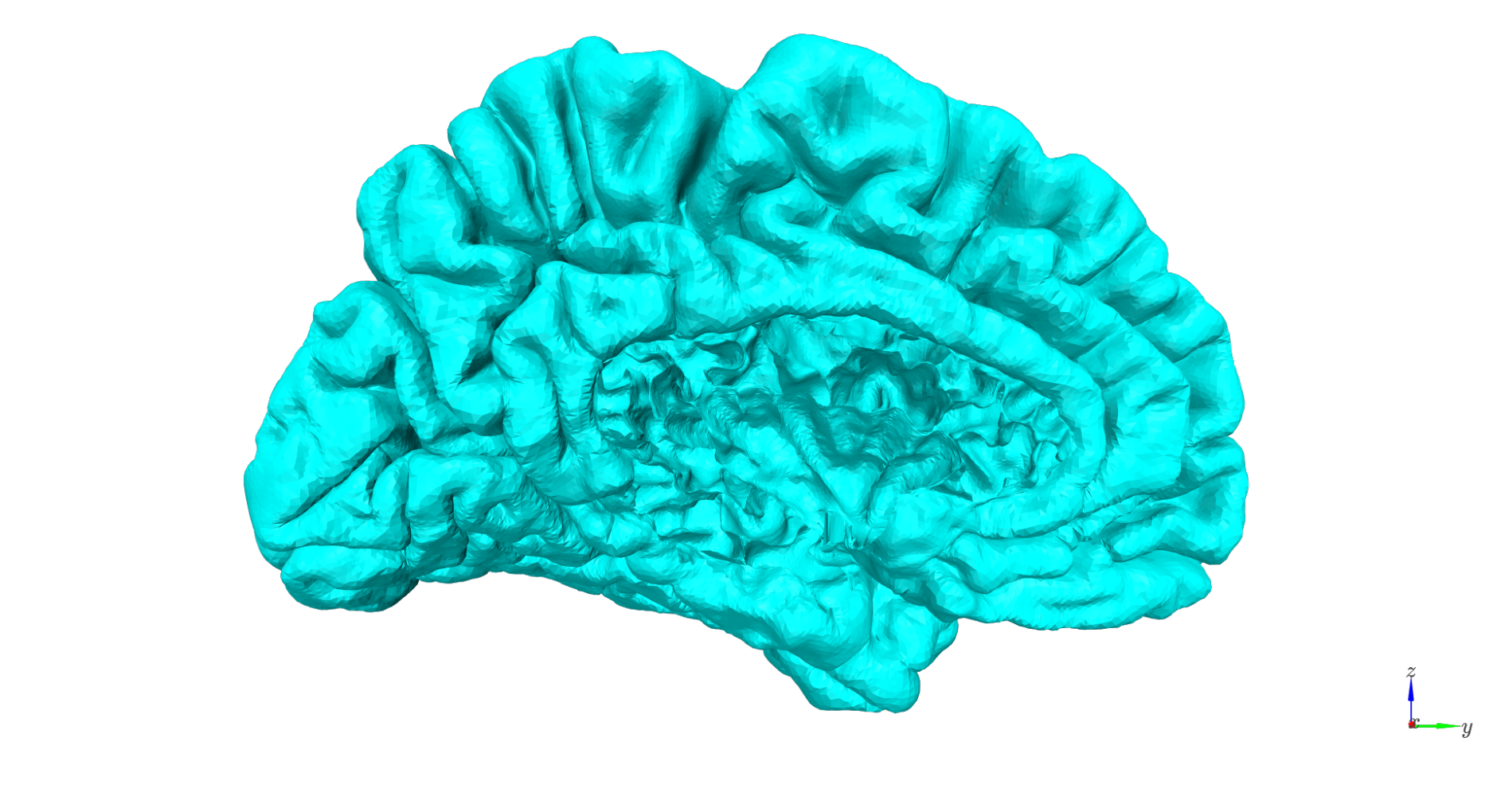
After: deep vertices are removed, leaving only cortical surfaces.

plot = show_surface(
    surf_set,
    layer_name='pial',
    stage='nodeep',
    hemi='lh',
    plot_curvature=False,
    camera_view=cam_view,
    color=col_r[0,:3]*255
)

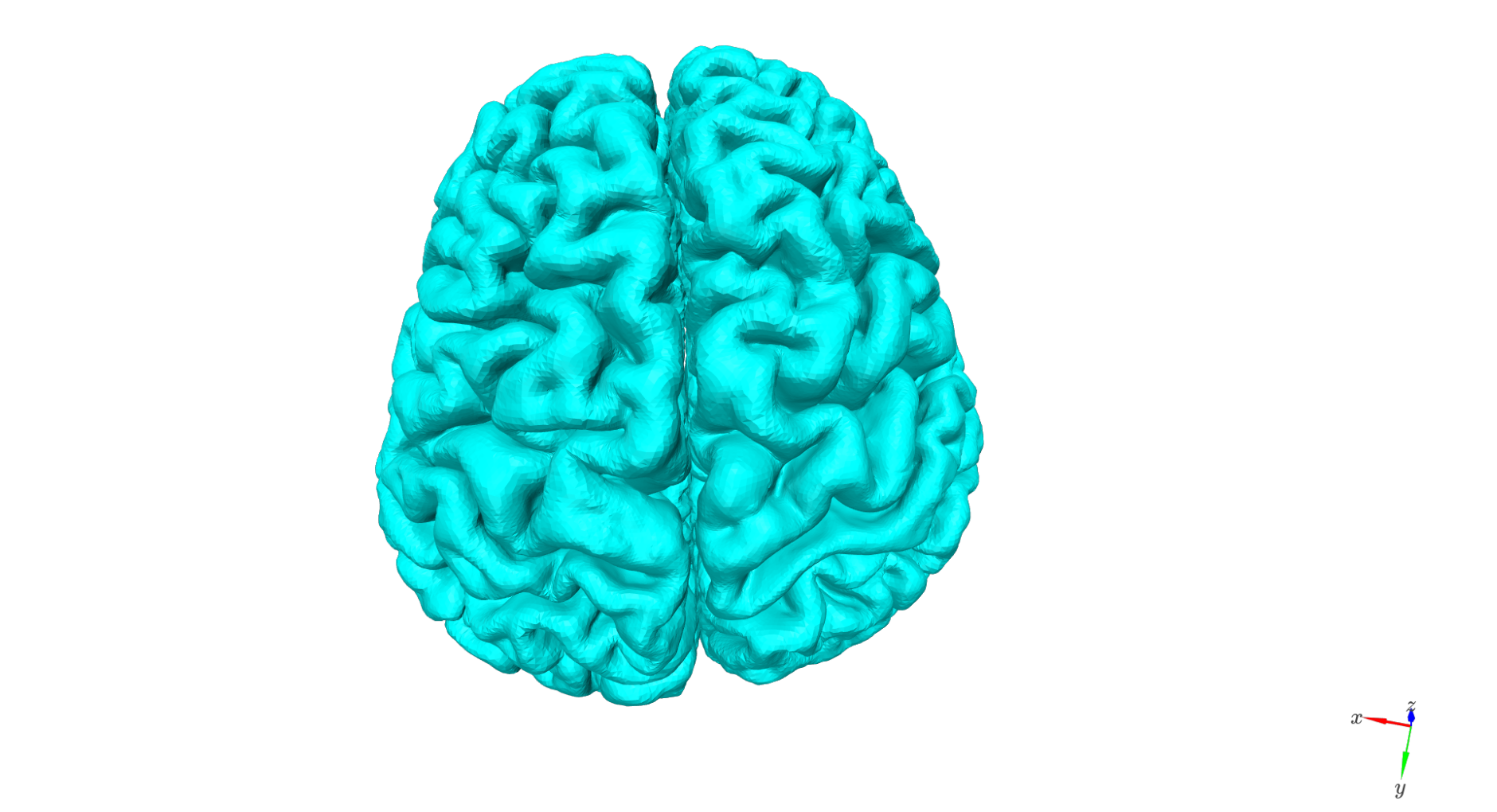
Combine hemispheres#

FreeSurfer outputs the left and right hemispheres separately. To facilitate visualization and later source modeling, we merge them into a single mesh.

This step: - Concatenates vertex and face arrays (left first, then right). - Does not introduce any new faces - hemispheres remain disconnected but stored together. - Is applied independently to each cortical layer.

cam_view=[13, 64, 217,
          21, 21, 33,
          0, 1, 0]
plot = show_surface(
    surf_set,
    layer_name='pial',
    stage='combined',
    plot_curvature=False,
    camera_view=cam_view,
    color=col_r[0,:3]*255
)

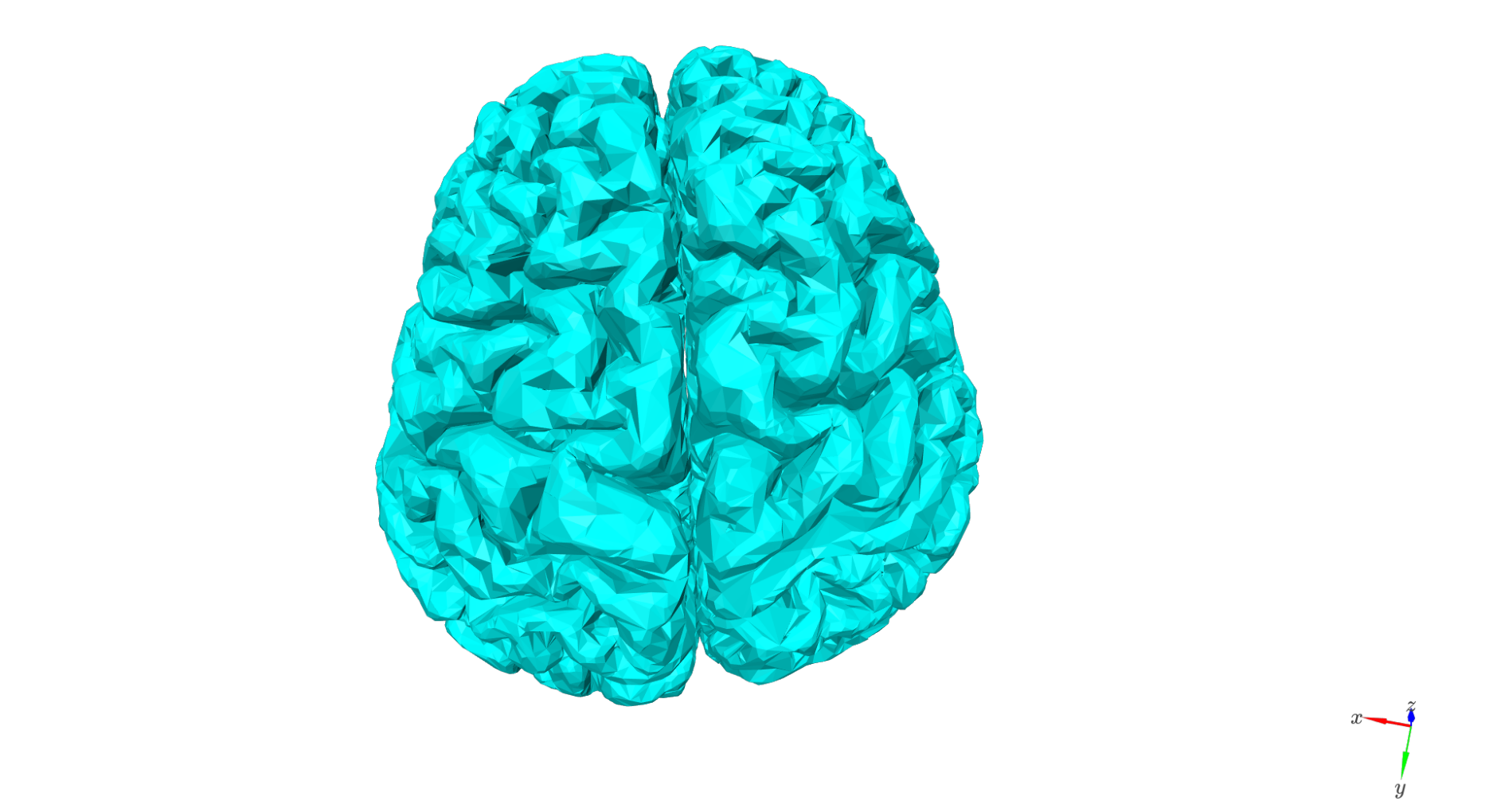
Downsample#

The original FreeSurfer meshes contain hundreds of thousands of vertices - far too dense for efficient source inversion. We therefore downsample the mesh while preserving vertex correspondence across layers (see [Bonaiuto et al. 2020, Estimates of cortical column orientation improve MEG source inversion](https://doi.org/10.1016/j.neuroimage.2020.116862)).

To achieve this: - The pial surface is downsampled using VTK’s DecimatePro algorithm, which removes vertices rather than creating new ones. - The same vertex indices are then removed from every other layer to maintain correspondence. - The face structure from the downsampled pial surface is propagated to other layers.

This ensures that each vertex index corresponds to the same cortical column across depth.

plot = show_surface(
    surf_set,
    layer_name='pial',
    stage='ds',
    plot_curvature=False,
    camera_view=cam_view,
    color=col_r[0,:3]*255
)

Combine layers#

Finally, all layers are merged into a single structure by concatenating their vertices and faces (from pial to white matter). No inter-layer connections are created.

The resulting surface set provides a compact representation of the cortical ribbon, where each vertex index corresponds to a single cortical column sampled at multiple depths.

plot = k3d.plot(
    grid_visible=False, menu_visibility=False, camera_auto_fit=False
)

for l_idx, layer_name in enumerate(layer_names):
    surface = surf_set.load(layer_name=layer_name, stage='ds')
    vertices, faces = surface.agg_data()

    mesh = k3d.mesh(vertices, faces, side="double", color=int(rgbtoint(col_r[l_idx, :3] * 255)),
                    opacity=l_idx / (surf_set.n_layers - 1))
    plot += mesh

plot.camera = cam_view

plot.display()

Putting it all together#

All the above steps - surface inflation, deep vertex removal, hemisphere merging, downsampling, and orientation computation - can be performed automatically using:

```python from lameg.surf import LayerSurfaceSet

surf_set = LayerSurfaceSet(‘sub-104’, n_layers=11) surf_set.create(

ds_factor=0.1, orientation=’link_vector’, fixed=True

)#

This function allows flexible specification of the number of intermediate layers, downsampling ratio, and dipole orientation model.

# Create a 2-layer surface (only pial and white)
surf_set = LayerSurfaceSet('sub-104', 2)
surf_set.create(
    ds_factor=0.1,
    orientation='link_vector'
)

# Create an 11-layer surface
surf_set = LayerSurfaceSet('sub-104', 11)
surf_set.create(
    ds_factor=0.1,
    orientation='link_vector'
)

# Create a 15-layer surface
surf_set = LayerSurfaceSet('sub-104', 15)
surf_set.create(
    ds_factor=0.1,
    orientation='link_vector'
)

Total running time of the script: (0 minutes 0.000 seconds)

Gallery generated by Sphinx-Gallery